The purpose of a servo control loop is to minimize error, and this is often done through the use of PID (proportional-integral-derivative) gains, which correct errors between the target value and the actual value. But the PID algorithm is reactive, and takes time to respond. Case in point: the proportional term requires an error in order to generate an output, and the integral term requires both an error and time. In addition, it’s not always possible to increase the PID gains to a level that results in acceptable error without causing instability in the system. One solution to both the reactive nature of PID gains and their tendency to cause oscillations at high levels is to use feed-forward gains.
In PID control, the proportional term is multiplied by the error between the target and actual values at any instant in time and generates the proportional contribution to the output for the next time period. Therefore, the proportional term is only useful once an error has developed.
Likewise, the integral term is multiplied by the sum of errors over time to generate the integrator contribution to the output. In other words, the integral terms needs time to build up, which hinders the responsiveness of the system.
Instead of being reactive, feed-forward control is proactive. It injects a command into the control loop based on the predicted error, without waiting for an error to develop or for the integrator term to build up.
Types of feed-forward
Feed-forward gains are an important tool for increasing system responsiveness, and since they work outside of the feedback loop, they don’t cause instability. Rather than being reactive, like PID gains, feed-forward gains are predictive and nearly instant, allowing faster response to command signals. Feed-forward control estimates the ideal output from the PID algorithm, then adds auxiliary signals to the servo loop, which allows the output to respond much more quickly.
There are two primary types of feed-forward: velocity feed-forward and acceleration feed-forward. Velocity feed-forward (Vff) minimizes error during the constant velocity portion of the move and works against viscous friction (friction that’s proportional to velocity).
Acceleration feed-forward (Aff) minimizes error during acceleration and deceleration and compensates for inertia in the system. (Recall that inertia causes an object to resist any change in velocity).
The target speed and acceleration values are multiplied by the velocity and acceleration feed-forwards in order to determine the total contribution to the control loop.
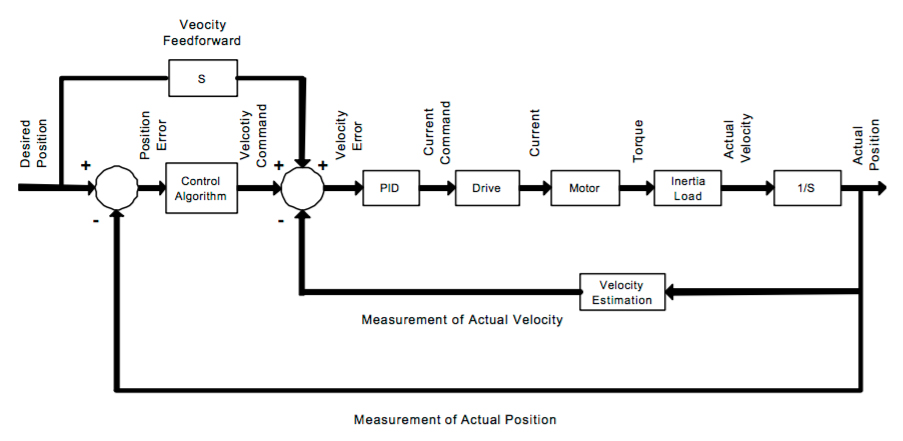
Image credit: Integrated Industrial Technologies, Inc.
Mathematical modeling
In an ideal servo system, the process variable (the variable being measured, such as velocity or position) will equal the set point. With the plant model (the system being controlled) being represented by the function Gp(s), feed-forward control can be described mathematically as:
SP(s) * FF(s) * Gp(s) = PV(s)
SP(s) = set point
FF(s) = feed-forward
Gp(s) = plant model
PV(s) = process variable
The feed-forward gains are the inverse of the plant function, making FF(s) * Gp(s) = 1, so the equation reduces to:
SP(s) = PV(s)
In other words, the process variable equals the set point and there is no error.
Dynamic applications need rapid response in order to avoid overshooting and long setting times. But the ability to increase the PID gains is limited by their tendency to cause instability. Feed-forward gains improve the system’s response by predicting the needed commands to achieve zero error, rather than waiting for the PID gains to respond to a past error. This leaves the PID gains to compensate for effects that can’t be predicted, such as varying loads or forces.


Leave a Reply
You must be logged in to post a comment.