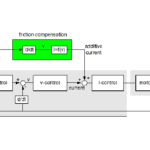
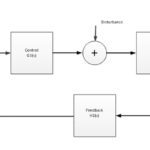
One way to improve servo system performance is to increase the gains in the control loop, allowing the system to respond faster to commands and to settle more quickly, with less oscillation. But increasing the servo gains means that any resonances in the system — typically due to mechanical compliance — are further amplified, which can cause instability and vibration. Another way to improve performance is to reduce or eliminate resonances by implementing filter circuits in the servo control loops.
Most servo system filters are based on a type of filter known as the biquad, or bi-quad (short for biquadratic). Biquad filters are expressed mathematically as the ratio of two quadratic functions, with the numerator representing the zeros and the denominator representing the poles. (For an in-depth explanation of poles and zeros in control theory, take a look at this article from MIT.)
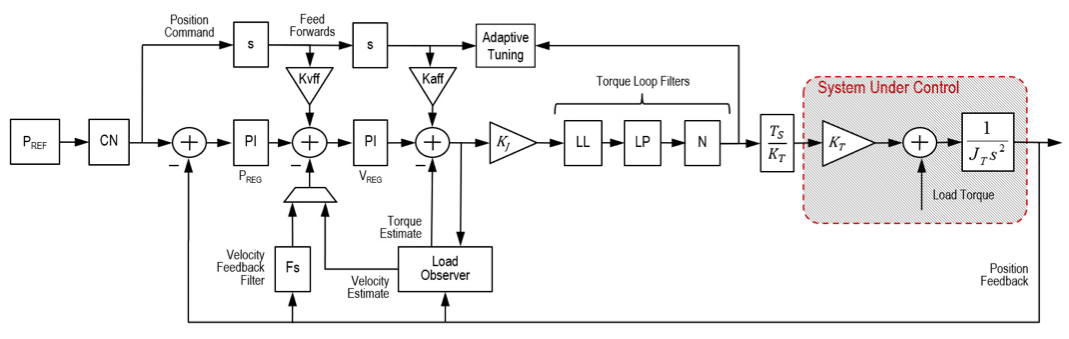
Image credit: Rockwell Automation
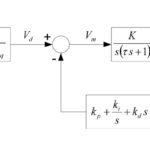
To find the gain, or frequency response, of the biquad filter (that is, how the filter responds to a sinusoidal input of varying frequencies), the denominator of the biquad is subtracted from the numerator. The behavior of the biquad filter is also affected by the Q factor, or quality factor, which represents the ratio of energy stored to energy dissipated at resonance. The inverse of Q is the damping factor, so higher values of Q mean lower damping, and vice-versa. (When the frequency response is plotted, the value of Q is seen as the width of the “notch.”)
Biquad filters are flexible and serve as the basis for constructing other types of servo tuning filters, including low-pass, notch, and lead-lag filters.
A low-pass filter allows signals below a corner, or cut-off, frequency to pass through, but attenuates signals above the corner frequency. Low-pass filters are commonly used in servo control systems because they can reduce the effect of resonances over a wide range of frequencies. But they also reduce system bandwidth, which can be detrimental to servo responsiveness.
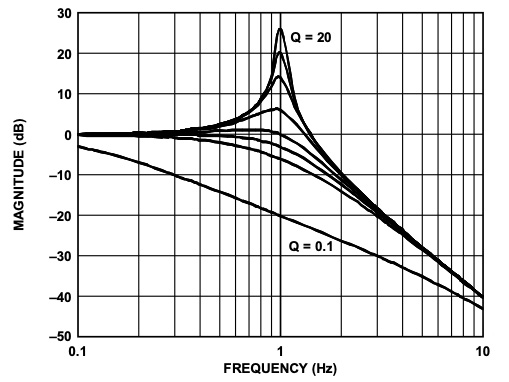
Image credit: Analog Devices
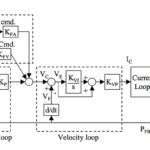
Notch, or band rejection, filters attenuate frequencies based on a center, or notch frequency and a bandwidth. The notch filter heavily attenuates frequencies around the center frequency — with maximum attenuation at the notch frequency — but attenuation drops off significantly near either end of the bandwidth range. Notch filters can be used to suppress both load-side and motor-side resonances and are typically implemented when the resonant frequencies are higher than the bandwidth of the control loop, but they can also be used when the resonance occurs near the control loop bandwidth.
Servo control algorithms often include two or more notch filters, and these are commonly used in conjunction with a low-pass filter. Because notch filters are used to attenuate specific frequencies, the resonance frequencies must be accurately identified, and if resonances change over time, notch filters can become ineffective.
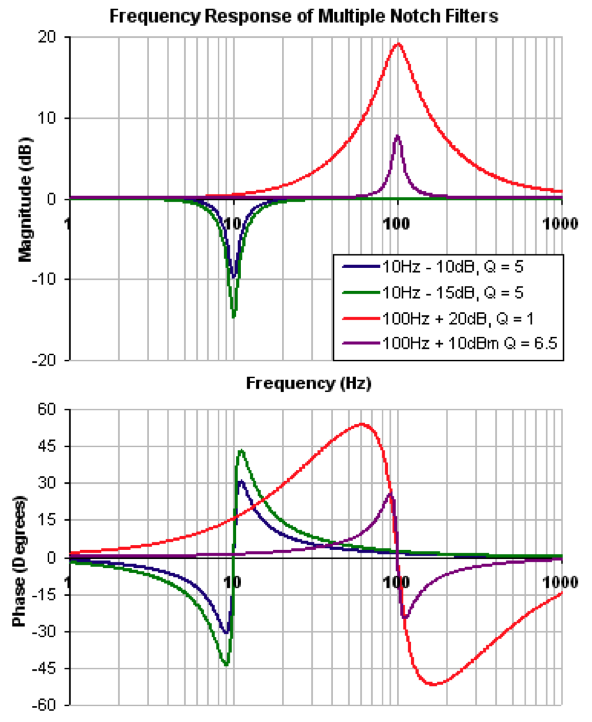
Image credit: Kollmorgen
Lead-lag filters provide attenuation at higher frequencies, but have no gain at lower frequencies. These filters are specified by their high-frequency gain, along with the frequency and gain at which the transition occurs. (For a great tutorial on lead-lag filters, check out this video by control systems engineer Brian Douglas.)


Leave a Reply
You must be logged in to post a comment.