The purpose of motion control is to move an axis, or multiple axes, to a specified position or through a predefined path. For the first case, some form of point-to-point positioning is used. For motion that must pass through a predetermined set of points, a method known as contouring is used. The choice between point-to-point or contoured motion depends on the application and process. The smooth shapes generated by contouring are important for CNC applications such as cutting, welding, and routing, as well as for dispensing applications where a specific path must be followed. Point-to-point motion is used in pick-and-place, assembly, and discrete dispensing applications.
Point-to-point motion
In point-to-point motion, the end position is designated, but the path used to reach the end position is irrelevant. Velocity, time, and acceleration can be defined for point-to-point moves, allowing the controller to construct either a trapezoidal or an s-curve move profile.
The simplest form of point-to-point motion, referred to as axial or single-axis motion, moves each axis individually. For example, to move from point 0,0 (X,Y) to point 120, 300 (X,Y), the X axis would move 120 mm. Then, once the X axis reached its position, the Y axis would move 300 mm. Because this is the slowest method, it is often replaced by multi-axis motion.
In multi-axis motion (also known as vector motion), two or more axes are coordinated to move at the same time in order to achieve the shortest path between the starting and ending points. Again, the path does not matter, only the end point. (As we’ll discuss later, this is a major distinction between point-to-point multi-axis motion and linear interpolation.)
Another type of multi-axis movement that falls under the point-to-point category is blended motion. With blended motion, the end of one move profile is joined with, or overlapped by, the beginning of the next move profile to create continuous motion between the two profiles. An example of blending is a 90 degree X-Y move in which the Y axis starts to move at a specified time before the X axis completes its move, resulting in a radius instead of a sharp corner.
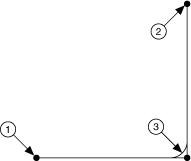
2. End point
3. Corner rounded by blending
Image credit: National Instruments
As mentioned earlier, point-to-point moves can be made with either a trapezoidal or an S-curve move profile. A trapezoidal move profile consists of an acceleration phase, a constant velocity phase, and a deceleration phase. Because of the sudden end of the acceleration phase, and the sudden beginning of the deceleration phase, trapezoidal profiles can create theoretically infinite jerk (rate of change of acceleration), which causes vibrations, increased settling time, and a loss of positioning accuracy.
When a trapezoidal move profile has a constant velocity time of zero (all the move time is spent accelerating and decelerating), it becomes a triangular move profile.
The S-curve move profile reduces jerk by incorporating seven phases of motion, which smooths the transitions between changes in acceleration rates. A graph of acceleration during an S curve move shows that the changes in acceleration follow a trapezoidal path, with ramps between each phase, whereas the changes in acceleration for a trapezoidal move are instant.
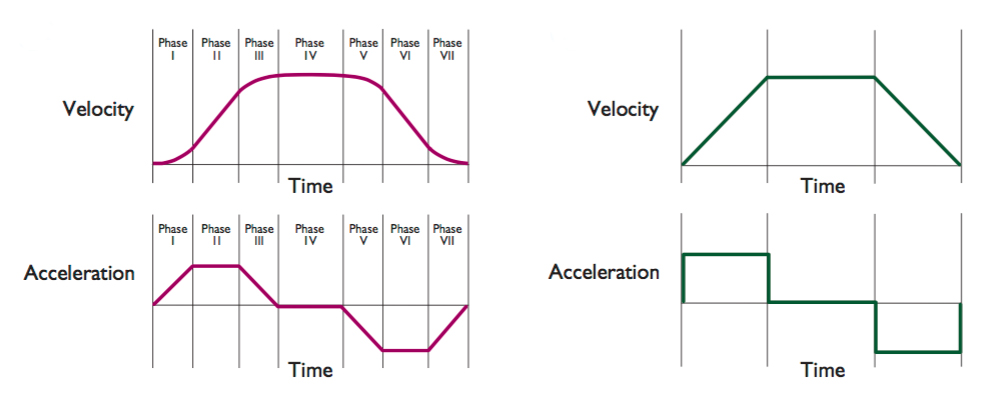
Image credit: Performance Motion Devices, Inc.
Contouring
To achieve contoured motion, a series of points is provided during programming, and the motion controller extrapolates a smooth line or curve from these points. Unlike point-to-point motion, contouring guarantees that the system passes through each point, using either linear or circular interpolation. In a contoured move, a time to complete the move is specified, but the actual move profile is determined by the motion controller.
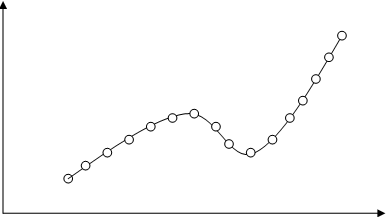
Image credit: National Instruments
Linear interpolation is used when the desired move is a straight line involving two axes of motion. The controller synchronizes the motion of both axes, calculating a series of very small moves along each axis that result in a straight line when executed. Keeping with the premise of contouring, linear interpolation (unlike multi-axis motion) ensures that the axes pass through each of the specified points.
Circular interpolation works much the same way as linear interpolation, but also requires the specification of a center point, radius, and direction (clockwise or counterclockwise) so that the motion created is circular rather than linear. In either type of interpolation, the speed of the movement (linear or circular) is also defined.
Because the motion path is critical for creating accurate contours, servo controllers for contouring applications typically use PID algorithms and incorporate advanced features, such as feedforward control, acceleration control, and high-speed processing capabilities.


Leave a Reply
You must be logged in to post a comment.