AMETEK Haydon Kerk Pittman (HKP), a business unit of AMETEK, has released a new size in its IDEA Motor series of brushless dc motors: 57 mm. This EC057B joins the 42-mm EC042B product introduced in 2019 and enhances a line of motors with integrated, programmable drives. The IDEA Motor combines a precision brushless servo motor […]
DC Motors
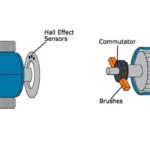
Which types of DC motors can be used as servo motors? (And a refresher on DC motor technologies)
Servo motors are used in applications where precise control of position, speed, or torque is required. But many different types of motors can be considered servo motors — the defining feature of a servo motor is that it incorporates or reads feedback in a closed-loop system. In fact, although many servo applications use synchronous AC motors, […]
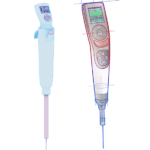
Successful lab experiments start with the right pipette motor
For medical lab applications, motor selection is integral to an electronic pipette’s accuracy and precision. Valentin Raschke Application Engineer Portescap Laboratory automation has always been a great fit for linear motion. Within certain laboratory devices, precision is required for moving samples into position, adding reagents, and withdrawing samples. Advancements in the linear force and speed […]
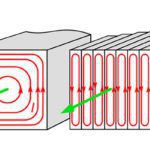
What are eddy currents and how do they affect motor performance?
One of the electromagnetic principles that governs the operation of an electric motor is Faraday’s law, which states that when the magnetic environment of a coil of wire is changed — whether by moving the magnet and coil relative to each other or by changing the magnetic field — a voltage, or electromotive force (EMF), will […]
Portescap integrates driver into new mini brushless dc motor
Portescap’s new 22ECP miniature brushless dc motor includes an integrated driver to optimize motor performance and simplify installation. The new 22-mm diameter motor is just 35 mm in length and delivers 50 percent more continuous torque than comparable brushless slotless miniature motors, without compromising smoothness of operation or motor lifespan. The new motor is the […]
Electric motors from maxon help Emirates Team New Zealand win 36th America’s Cup
Emirates Team New Zealand has won the historical 36th America’s Cup that endured extra challenges — including COVID-19, race cancellations, and delays that caused interruptions and last-minute tactical changes. The Kiwis have retained the oldest trophy in international sporting history. Creating a boat from simulation and the use of AI technology were big risks for Emirates […]
Compact, energy-efficient brushless dc motor for high-speed applications
Portescap has added the 16ECS high-speed brushless motor to its Ultra EC mini brushless dc motor platform. These compact 16-mm motors are available in 36- and 52-mm lengths and provide high power while running at speeds of 75,000 rpm. The 16ECS is comprised of an enhanced magnetic circuit that reduces iron and recirculation losses that […]
Swiss precision motors handle valuable Mars soil samples
Was there once life on Mars? This is the question that one of the most complex robotic systems ever built by humankind has set out to answer. Several of maxon’s electric drives are used for handling the soil samples — and to control the first Mars helicopter. The rover named Perseverance entered the atmosphere of […]
Micro motors give robotic hand a boost
Among the changes to small motor design over the years has been the use of powerful rare-earth magnets to increase power density, making for smaller and more powerful motors. These motors are finding their way into medical devices, robotics, as well as the intersection of these two. Case in point; a robotic glove. Ironhand from […]
Brushless DC motor from Portescap with integrated driver saves you space and time
Portescap introduces the newest addition to their Ultra EC mini brushless DC motor platform – the 16 ECP brushless motor with a new integrated driver. These new 16mm diameter motor versions are available in two lengths (36mm & 52mm). These compact motors offer almost 50 percent more continuous torque over similar comparative motors without compromising […]
