Torque is a rotational force produced when a vertical force is applied at some distance from the center axis of the rotating body. The familiar equation for torque is:
![]()
Where:
T = torque
F = applied vertical force
d = distance from axis of rotation
In a DC motor, the output torque is directly proportional to the current through the windings, and is given as:
![]()
Where:
I = current through the windings
kT = torque constant (specific to the motor)
To see how this relationship is developed, let’s look at the geometry of a DC motor:
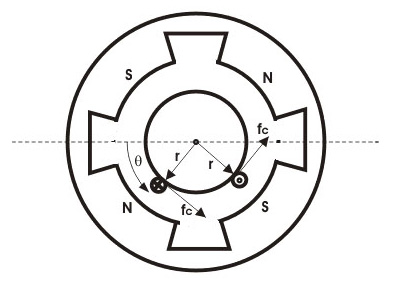
Image credit: electrical4u.com
The force on one coil is the product of flux density, current through the coil, and the length of the coil:
![]()
Where:
Fc = force on one coil
B = flux density
Ic = current through one coil
L = length of the coil
The current through one coil is calculated as:
![]()
Where:
Ia = total current through the armature
A = area of the coil
Substituting for Ic in the force equation, we get:
![]()
Because torque equals force times distance, the torque equation can be shown as:
![]()
Where:
Tc = torque on one coil
r = distance from center of armature
The flux density, B, equals the total flux divided by area:
![]()
Where:
φ = total flux
Because the motor is essentially a cylinder, area is calculated as:
![]()
Where:
P = number of poles
Substituting into the flux density equation, we get:
![]()
Substituting this into the torque equation, we get:
![]()
Which simplifies to:
![]()
Tc is the torque on just one coil. Total torque equals Tc multiplied by the number of coils:
![]()
Where:
T = total torque
Z = number of coils
To further simplify the torque equation, the number of poles (P), the number of coils (Z), and the geometric factors (2πA) can be combined to form the torque constant, kT, which is specific to the motor. This simplifies the torque equation to:
![]()
For most DC motor cases, we can assume the flux, φ, is constant, making torque directly proportional to the current:
![]()
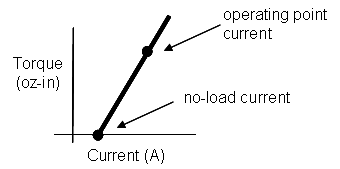
When examining the torque-current curve for a DC motor, notice that the no-load (stall) current is greater than zero. This is because some current is needed to overcome the internal friction of the motor.





Leave a Reply
You must be logged in to post a comment.