In any drive system (that is, a motor driving a load), there is going to be inertia. Specifically, the motor will have inertia as will the load. For a direct drive system (a direct motor-to-load connection) the individual inertias can just be added together in a straightforward way. However, for any other type of setup involving some additional mechanical drive components such as couplings or gears, the relationship changes.

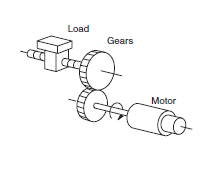
Specifically, when looking at how gears impact a drive system’s inertia, there are some basic ways to look at it. The basics; any gear will reduce the load inertia reflected to the motor by a factor of the square of the gear ratio. When looking at a gearmotor, this is basically just a motor with an embedded gearset in it, so the calculations and formulas for calculating inertia are the same.

In high performance motion control applications, it’s ideal for the reflected load inertia to equal the motor inertia. If inertia matching is the only concern, then the gear ratio can be calculated as:

N = √ (J_Load/ J _Motor)

where N is the gear ratio, J_Load is the inertia of the driven load, and J_Motor is the inertia of the motor.

Note: Another way to calculate gear ratio is by reference to the individual gears. For instance, if N_In is the number of gear teeth on the input gear and N_Out is the number of gear teeth on the output gear, the gear ratio is then:

N = N_Out / N_In

As for reflected inertia itself, this is best understood as the inertia of the load that is translated back to the motor through various drive components, in this case the gearing of the gearmotor.

So in a simple direct-drive system, the total inertia would be calculated like this:

J_Total = J_Load + J_Motor

However, for a geared drive system such as a gearmotor, the total inertia is calculated using the equation:

J_Total = ( J_Load / N² ) + J_Motor

This is because, as stated earlier, the reflected load inertia is equal to the load inertia divided by the square of the gear ratio.

Update: Click here to read an update to this article with a few important corrections.