Selecting an appropriate retaining ring for an application typically involves evaluating factors such as installation stress, the radial load exerted by the ring, and the thrust capacity of the ring. And because the groove that holds the ring is integral to the ring’s performance, groove deformation needs to be considered as well.
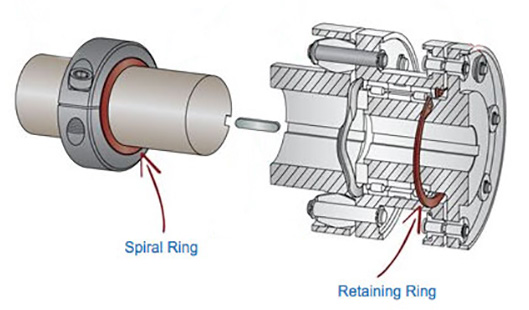
But when an external retaining ring is used on a rotating shaft, centrifugal forces can cause the ring to lift out of its groove, leading to ring failure, so maximum speed becomes an important selection factor as well.
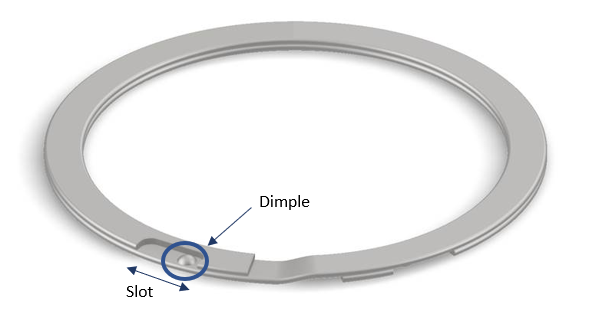
Image credit: Smalley
The maximum speed that an external retaining ring can withstand is the speed at which the force holding the ring in its groove becomes zero, and is determined by the ring’s material properties and size.
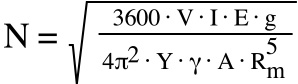
N = maximum rotational speed (rpm)
3600 = conversion from rotations per second to rotations per minute (square root of 3600 = 60)
V = radial interference between ring and groove, also referred to as “cling” (in)
![]()
DG = groove diameter (in)
DI = ring inside diameter (in)
I = planar moment of inertia (in4)
Because the ring has a rectangular cross section, we use the planar moment of inertia (also referred to as second moment of area) formula for a rectangle, using the ring’s thickness and section width as the base and height of the rectangle.
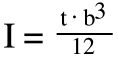
t = ring thickness (in)
b = ring radial section width, or wall (in)
E = modulus of elasticity (psi) = 29 x 106 psi (for most steels, excluding stainless alloys)
g = acceleration due to gravity (in/s2) = 386.4 in/s2
4π2 = factor to convert to revolutions (square root of 4π2 = 2π, which is the number of radians in one revolution)
Y = factor for number of turns (1 turn = 1.909, 2 turns = 3.407, 3 turns = 4.958)
Spiral retaining rings can have more than one turn, or coil, around the ring’s diameter. Typical constant section and tapered rings have only one turn, so for these designs, the factor for one turn (1.909) is used.
γ = material density (lb/in3) = 0.283 lb/in3 (for most steels, excluding stainless alloys)
A = cross-sectional area (in2)
![]()
Rm = mean free radius (in)
![]()
For retaining rings made of most steels and steel alloys, except stainless versions, the known quantities can be combined, and the equation can be simplified to:
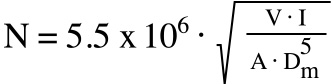
Note that in the denominator, we’ve used mean diameter, rather than the mean radius.
![]()
Dm = mean free diameter (in)
Image credit: Rotor Clip
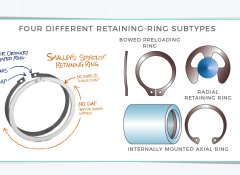
To address applications that run at high speed, retaining ring manufacturers have developed external rings with self-locking features that prevent the ring from failing, even under high centrifugal forces.
One design, used for spiral-wound retaining rings, incorporates a raised dome on the inside turn of the ring and a slot on the outside turn. As speed increases and the ring begins to expand, the dome slides along the slot, and the length of the slot limits the amount by which the ring can expand. Another design, used on traditional retaining rings, features a two-piece ring whose ends interlock when assembled onto a shaft, preventing the ring from expanding.






Leave a Reply
You must be logged in to post a comment.