Servo drives, also called amplifiers in the motion-control industry, take a command signal for position, velocity, or current and adjust the voltage and current applied to the servomotor based on closed-loop feedback. In fact, a servo drive is just one element of a motion control system, which includes a servo motor, the drive, controller, and some type of feedback element.

The signal sent to the servomotor needs to be amplified because control signals are too low (in terms of current levels) to power the windings of a motor, which require higher current levels in order to generate a sufficient amount of torque to do work, or move a load. (Keep in mind that for electric motors, torque is proportional to current.)

Servo-drive logic can include up to three types of servo loops – current, velocity, and position. These servo loops use feedback signals to adjust the output of the loop to produce the desired result.

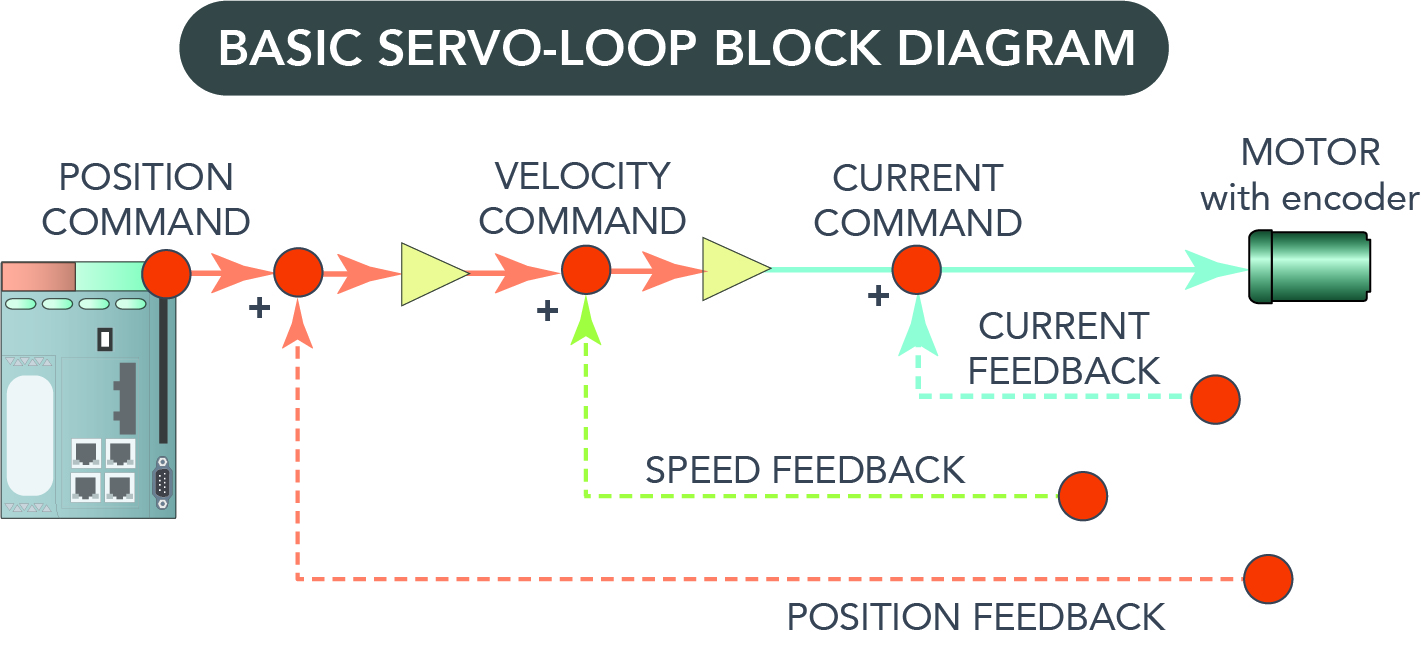
The current loop reacts to the commanded current requirement — which in turn can precisely control the motor’s torque output. In that case, the drive is considered a torque mode amplifier.

Likewise, the velocity loop uses feedback to adjust the motor to operate at the commanded speed by adjusting the command to the current loop.

The position loop will get a commanded position, and adjust its output to the velocity loop based on position feedback which in turn will adjust its command to the current loop based on velocity feedback. The servo loops are said to be nested – as each loop reacts and adjusts the command at each level.

Each loop has specific filtering elements that adjust or tune the loop for optimum performance. Many servo amplifiers include auto-tuning capabilities that help optimize servo performance based on the machine dynamics.



Article updated August 2019.