Understanding the torque equation and the relationship between speed and torque is an important part of selecting and operating a DC motor.

DC motors are relatively simple machines: when the load on the motor is constant, speed is proportional to supply voltage. And when supply voltage is constant, speed is inversely proportional to the load on the motor. This second relationship—between speed and load (or torque)—is typically shown on the motor’s torque-speed curve.

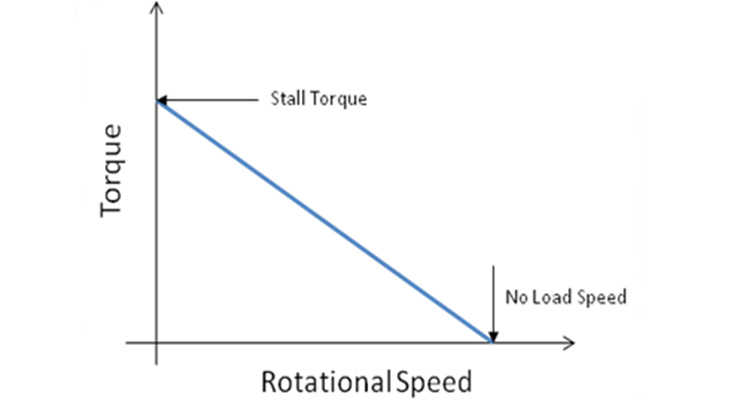
The inverse relationship between speed and torque means that an increase in the load (torque) on the motor will cause a decrease in speed. This can be demonstrated by the DC motor torque equation:

Where:

T = motor torque

V = supply voltage

ω = rotational speed

k = motor constant

R = resistance

Of course, the motor constant (k) doesn’t change, and resistance (R) in the motor windings is constant. Therefore, when supply voltage (V) is constant, torque (T) is inversely proportional to speed (ω).

Rearranging for speed, we can see the same inverse relationship to torque:

To see the derivation of the DC motor torque equation, check out this article.

The inverse relationship means that the torque-speed curve is a descending line, with a negative slope. The torque-speed curve begins at the crossing of the Y axis, where torque is maximum and speed is zero. This is the stall torque—the maximum torque when the motor is running at nominal voltage. The curve slopes downward until it intersects the X axis—that is, zero torque and maximum speed. This point is known as the no-load speed—the speed when running at nominal voltage and zero load.

Because the torque-speed curve is a straight line, it’s simple to find the torque that the motor can produce at a given speed, or conversely, to find the motor’s speed for a given load (torque) on the shaft. Recall the equation for a straight line:

Where:

y = value of y axis variable, to be determined

m = slope of the line; change in y divided by change in x

x = value of x axis variable, given

b = y intercept; point at which the line crosses the y axis

Using this equation for the torque-speed curve, we can find the motor’s torque at a given speed. In this case, the variables in the line equation represent the following:

y = torque to be determined

m = change in torque divided by change in speed

x = given speed

b = stall torque (value where the line crosses the y axis)

The line equation can also be rearranged to find the motor’s speed at a given torque: