Motor windings have a property referred to as inductance, which is a resistance to any change in the electrical current through the winding. The result of inductance is the production of back EMF to oppose the change in current.
![]()
Where:
Eb = back EMF (volts)
L = inductance (H, or Ohm-s)
dI/dt = rate of change of current
Note that the magnitude of dI/dt is expressed as frequency times current (ω x I). The value of frequency is given by:
![]()
Where:
ω = frequency (rad/s)
S = motor speed (rpm)
N = number of magnetic cycles per shaft rotation
The windings also have a resistance to the current flowing in them. This resistance is proportional to the square of the number of turns in the winding. According to Ohm’s Law, voltage equals current times resistance: V = I x R. Ohm’s law expressed in terms of resistance shows:
![]()
Where:
R = resistance (ohms)
V = voltage (volts)
I = current (amps)
While resistance and inductance are similar properties, resistance determines the maximum current in the winding, whereas inductance determines the maximum rate of change of current in the winding.
The electrical time constant is the amount of time it takes the current in the winding to reach 63 percent of its rated value. The time constant found by dividing inductance by resistance.
![]()
Where:
τe = electrical time constant (s)
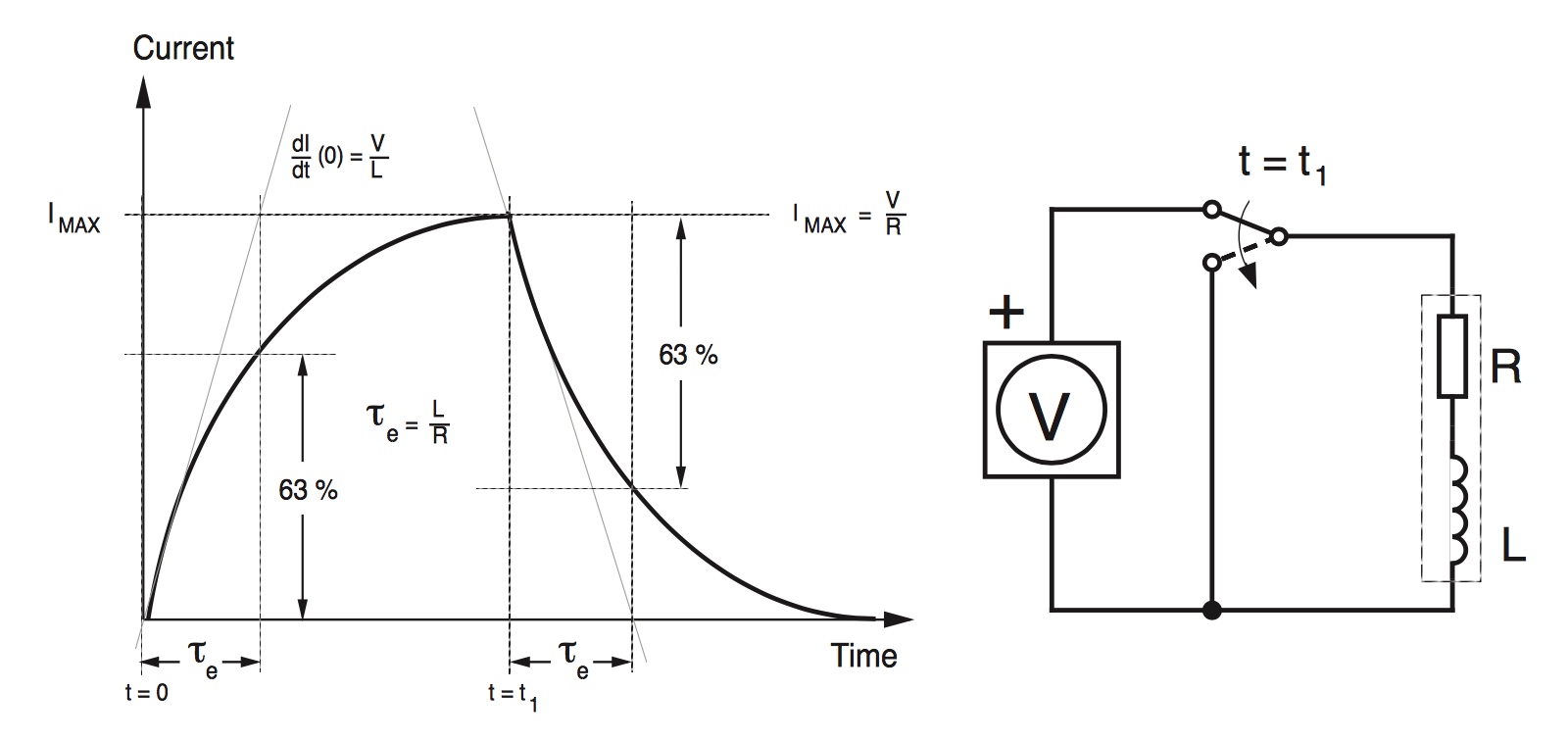
Image credit: NJR Co., Ltd.
Q: Why does the electrical time constant represent 63 percent of the maximum rated current (and not, say 50 percent or 85 percent)?
A: Because the time constant of an increasing system is the time that it takes the system’s step response (the resulting output when the input changes from zero to one very quickly) to reach 1 – 1/e of its final value. The value of 1 – 1/e is 0.632, or approximately 63 percent.
A lower time constant is usually desirable, because it means that current flows more quickly into the windings. This allows the motor to reach its rated torque before current is switched to the next phase. When the motor speed is high (high stepping frequency), there’s not enough time for the winding to receive sufficient current to produce the rated torque.
There are two ways to achieve high speed from a stepper motor: increase the rate of current flow, or decrease the time constant by keeping the inductance low. The first option, increasing the rate of current flow, requires increasing the voltage to the motor. While stepper motors can be run at higher than rated voltage, the higher voltage also means higher maximum current, which could cause the motor to overheat or the rotor to be demagnetized. So in this solution, some form of current limiting must be employed.
The second solution, using a motor with low induction (and therefore, a lower time constant), is a matter of motor selection. However, low induction means higher current, and a stepper drive with a higher current rating—and therefore, higher cost—will be required.





Leave a Reply
You must be logged in to post a comment.