Most precision stepper motor applications — especially those in automation and motion control — use a control method referred to as microstepping, which creates a sinusoidal (or nearly sinusoidal) current waveform, rather than the square wave of current produced with typical full-step control.
The current rating of a stepper motor depends on the amount of power and, therefore, heat that the motor windings can withstand. Power is directly related to resistance and to the square of current (P = I2R), so current is critical to motor heating. (Keep in mind that resistance is a property of the motor windings, so it remains constant for a given motor.)
To quantify the amount of heating inside the motor, we use the average power — and therefore, the average of I2 — delivered to the motor over time. But because the sinusoidal waveform of microstepping control means that current is constantly changing over time and reversing direction (from positive to negative) — much like an AC current waveform — we need to use the time varying average of the current, which is the root mean square, or RMS, current value.
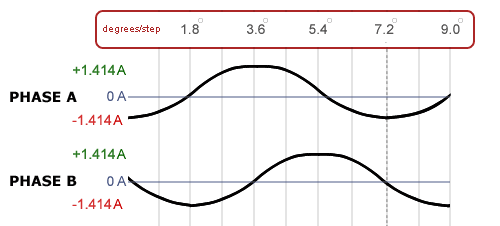
Image credit: AMCI
The RMS value of an AC current waveform represents the amount of DC current that would be needed to produce the same amount of heating when flowing through the same resistance.
Root mean square is a statistical method of finding the mean, or average, of a set of values. To find the root mean square, first square each value and sum the squares. Then divide the sum by the number of values. This gives you the mean. Finally, take the square root of the mean, and the result is the RMS value.
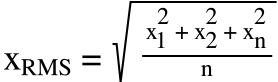
The relationship between RMS current and peak current is:
![]()
![]()
This is easy to visualize using the geometry of a right triangle, as shown in this post from Lin Engineering.
In short, if you plot a simple stepping sequence (this example uses 8 steps), with Phase A current on the X axis and Phase B current on the Y axis, you can see that the maximum, or peak, current along the step sequence in either phase is 1.414 A, or 1.414 times the RMS current of 1 A. (This exercise works with any value of IRMS. For example, if IRMS is 3 A, Ipeak will be 3 * 1.414 = 4.242 A.)
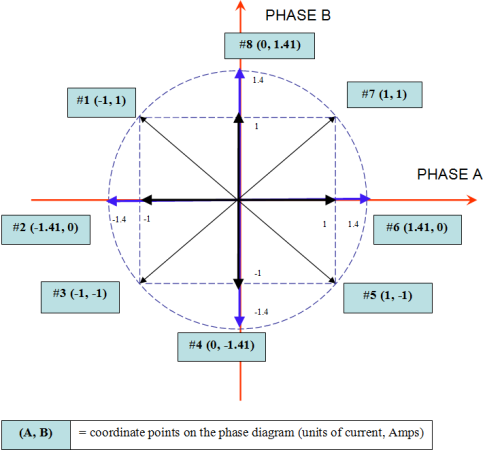
Looking at the triangle formed at position 7 and using the Pythagorean Theorem, you can derive the relationship between peak and RMS current:
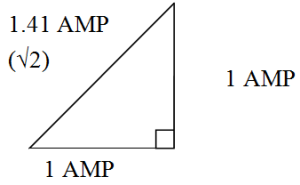
![]()
![]()
![]()
![]()
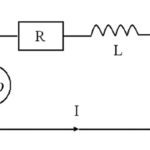
There are two fundamental types of stepper drives: L/R drives, which supply the motor with constant voltage, and chopper drives, which supply the motor with constant current. At high speeds, L/R, or constant voltage, drives have difficulty delivering enough current for the motor to reach the rated torque due to the time constant of the motor windings. This limits the use of L/R drives primarily to low-speed applications.
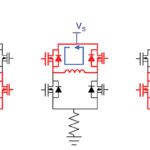
This is why many stepper motor applications use chopper drives and microstepping control. A chopper drive rapidly switches the voltage on-and-off (a method referred to as “chopping”) to control the amount of current to the motor. At the beginning of each motor step, very high voltage (typically eight times the motor’s nominal voltage) is applied to the windings, causing the current to rise very quickly and reach a higher level. The chopping frequency is controlled by pulse-width-modulation, so that a constant RMS value of current is supplied to the motor, regardless of the voltage.
To avoid exceeding a stepper motor’s peak current capability and to avoid possible motor damage, it’s important to pay attention to whether the motor’s current rating is given as peak or RMS and to the type of drive (L/R or chopper) being used.




Leave a Reply
You must be logged in to post a comment.