AC drives have historically been controlled by a scalar method known as volts per hertz (V/Hz), in which the drive maintains a constant voltage-to-frequency ratio in order to maintain stable torque production. However, the V/Hz control scheme doesn’t allow tight speed regulation and is limited in its ability to produce torque at low speeds. Vector control, on the other hand, enables more precise control of speed or torque, and is quickly gaining ground over V/Hz control in all but the most basic AC motor applications.
What is vector control?
The basic premise of vector control, also referred to as field oriented control (FOC), is to transform a three-phase system that is dependent on time and speed into a two-coordinate (d and q), time invariant system. It does this mathematically through the use of a Clarke transform and a Park transform.
AC motors have only stator windings (the current in the rotor is induced electromagnetically, hence the term induction motor) but there are two components to the stator current: the magnetizing current (d) and the torque-producing current (q). The magnetizing current lags the voltage by 90 degrees, and the torque-producing current is in phase with the voltage. Recognizing this relationship, a vector drive is able to control the two currents independently, much like the operation of a DC motor. Decoupling the torque and magnetizing currents allows independent torque control.
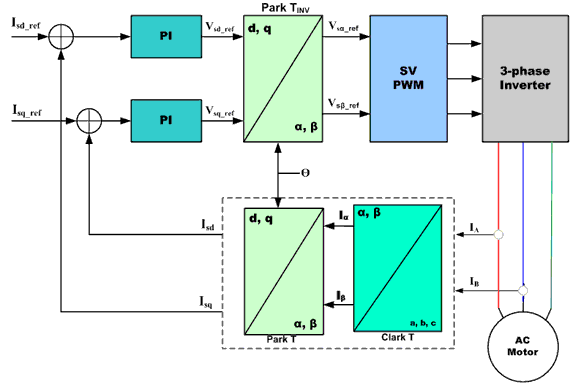
Image credit: Renesas
Closed-loop vector control
When an encoder is used in conjunction with a vector drive to provide shaft position feedback, the system is referred to as closed-loop. Information regarding the shaft position allows the controller to determine if the torque output is incorrect. That is, if the shaft overshoots the desired position, then too much torque is being applied, and vice-versa. Based on shaft position, the voltage can be adjusted to increase or decrease the torque, regardless of motor speed.
Open-loop vector control
Vector control without an encoder, often referred to as open-loop vector control, avoids the need for a feedback device by using a mathematical model of the motor operating parameters. Rather than using a shaft encoder to monitor position, the controller monitors the current and voltage from the motor. It compares these values to the model, and then makes error corrections to the supplied current, which in turn, adjusts the torque. Thus, open-loop vector control requires a very accurate motor model.
In this context, “open-loop” is a misnomer. The system is actually closed-loop, but the feedback information comes from within the VFD itself instead of from an external encoder. Therefore, open-loop vector drives are also referred to as “sensorless” vector drives.
Benefits and uses of vector control
Open-loop vector control provides tighter speed control, higher starting torque, and higher low-speed torque than simple V/Hz control, and does so without adding significant cost. A drawback to open-loop vector control is that it has difficulty monitoring current (and, therefore, making torque adjustments) at very low motor speeds. For this reason, open-loop control is not recommended for applications that require holding a load at standstill. It can, however, produce 100 percent of rated torque at speeds down to about 8 Hz, so it is sufficient for most applications that require high torque at low speeds.
The most significant benefit of closed-loop vector control is that it allows up to 200 percent of the motor’s rated torque to be produced at 0 rpm. This is especially useful in applications that require holding a load at standstill, such as cranes and hoists. Closed-loop vector control is also very similar to servo control, since the shaft encoder can provide accurate travel feedback.
Closed-loop vector control is required in processes where error accumulation should be avoided, such as web applications in the printing and converting industry.
Feature image credit: Rockwell Automation
Leave a Reply
You must be logged in to post a comment.