When a compressive or tensile load is applied to a spring (or any elastic material), the load does work on the spring, causing the spring to undergo a change in shape (extension or compression). This change in shape creates a type of potential energy — referred to as strain energy — in the material.
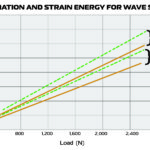
Typical compression springs experience both shear and torsional stresses and store strain energy from both stresses. Wave springs, however, experience only shear stress (no torsion) and therefore, have lower strain energy, meaning they can exert higher forces — or resist higher loads — than standard compression springs.
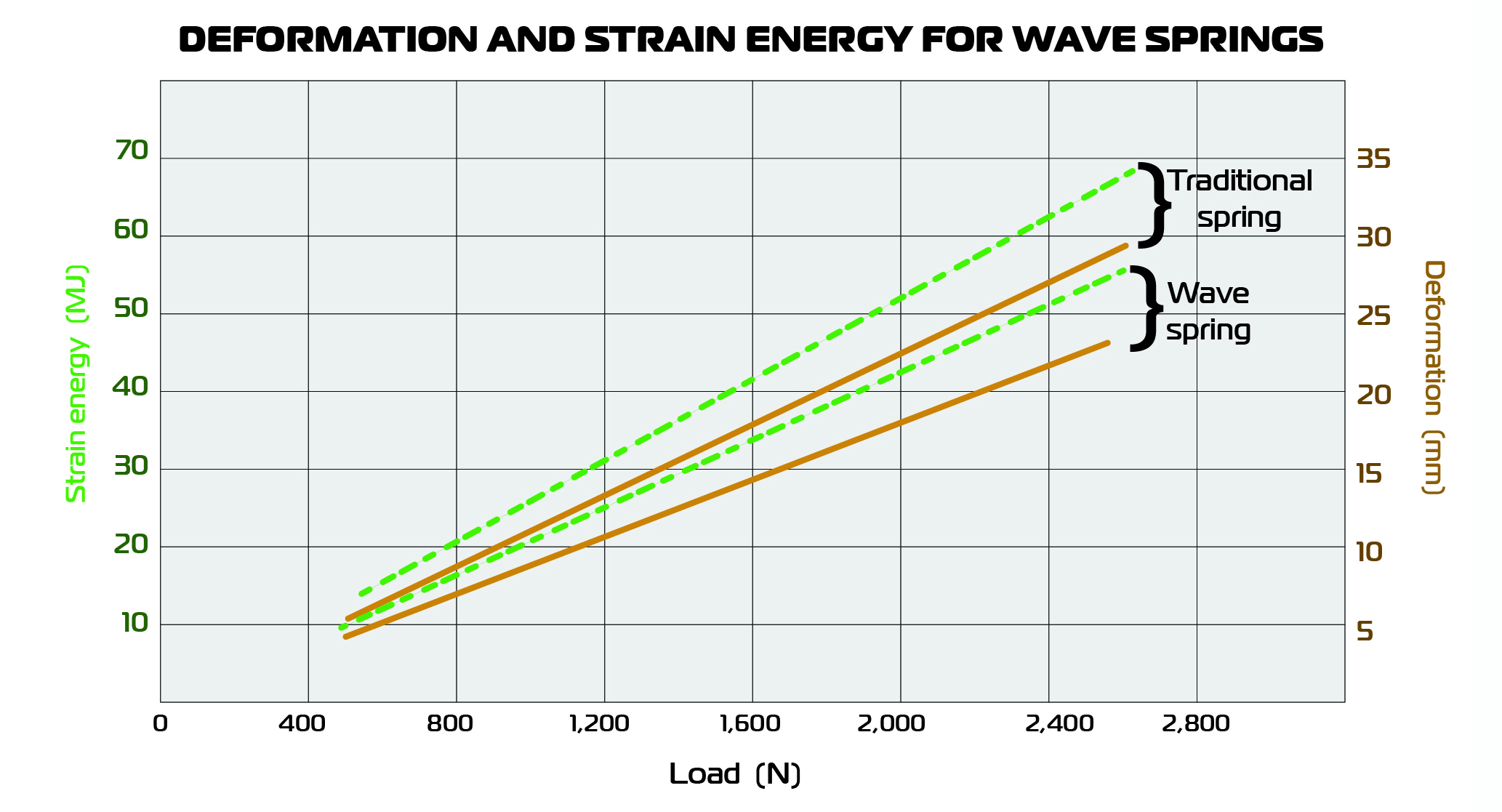
Data courtesy P. Ravinder Reddy and V. Mukesh Reddy
Stress is the applied load on a material divided by the material’s cross-sectional area. Stress causes the material to change its shape, and strain is the deformation that occurs due to stress.
Materials that follow Hooke’s law — which include most compression springs and wave springs — experience deflection, or displacement, in proportion to the applied force.
F = applied force (N)
k = spring constant (N/m)
δ = deflection (m)
Wave springs have relatively linear spring constants and provide consistent force over a range of deflections (or conversely, predictable deflection over a range of forces).
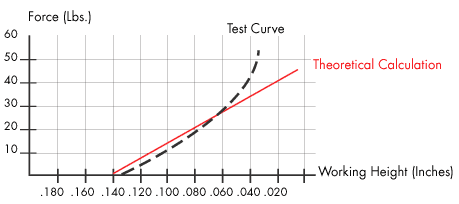
Image credit: Smalley
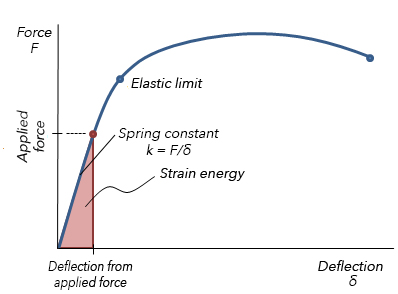
The behavior of a spring is often depicted in a force-deflection chart, which shows the amount of deflection the spring experiences for a range of forces. The slope of the force-deflection curve represents the spring constant, and the area under the curve is equal to the work done by the load to displace the spring. This work — force applied over a distance — represents the potential energy (strain energy) stored in the spring. (See note below for more on the work-energy relationship.)
From the spring equation above, substituting kδ for F…
U = strain energy (Nm, J)
δ = deflection (m)
F = applied force (N)
k = spring constant (N/m)
Strain energy is elastic — that is, the material tends to recover when the load is removed. The ability of a material to return to its original length or shape by releasing strain energy when a load is removed is referred to as its resilience. A spring with high resilience can withstand greater deflections and produce higher forces. The best performance comes from springs that have high allowable deflection (resilience) and high permissible forces.
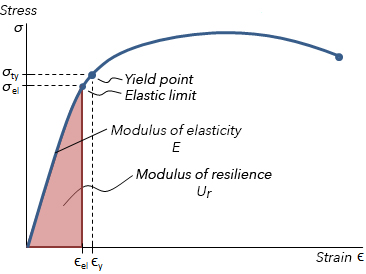
Resilience is typically expressed as the modulus of resilience, which is the amount of strain energy the material can store per unit of volume without causing permanent deformation. The modulus of resilience can be found by taking the area under the material’s stress-strain curve, up to the elastic limit (which is approximately equal to the yield point).
Ur = modulus of resilience (N/m2, Pa)
σy = yield stress (N/m2 Pa)
εy = yield strain (dimensionless)
E = modulus of elasticity (N/m2, Pa)
A note about work and energy
When work is done on an object, its energy is changed by an amount equal to the work done.
In the case of springs, it’s the potential energy (referred to as strain energy) that is changed. In other words, a spring’s strain energy is equal to the work done on the spring.
Leave a Reply
You must be logged in to post a comment.