If you design, install, or troubleshoot motion control systems, you’re probably familiar with PID (proportional-integral-derivative) control, which uses feedback to detect errors between the desired position and the actual position and applies corrective commands to compensate for those errors. Although PID control is the most common type of industrial controller, it does have limitations. First, PID control is generally not suitable for systems with multiple inputs and multiple outputs (MIMO), as the transfer functions and differential equations used to represent the system become overly complex when more then one input (or output) is involved. Second, PID control is based on constant parameters, so its effectiveness in controlling non-linear systems is limited.
An alternative control method is state space control. The key difference between PID control (aka “transfer control”) and state space control is that the state space method takes into account the internal state of the system, through what are referred to as “state variables.” These state variables describe the system and its response to any given set of inputs. PID control, on the other hand, relies on an “observer,” which estimates the internal state of the system based on measured inputs and outputs.
A state space system is represented by just two equations. First, the state equation gives the relationship between the system’s current state and input to its future state. The output equation gives the relationship between the system’s current state and input to its output.
For a linear time-invariant* (LTI) system, the state and output equations are as follows:
x’ = Ax(t) + Bu(t)
y(t) = Cx(t) + Du(t)
Where:
x is the vector of all the state variables
x’ is the time derivative of the state vector
u is the input vector
y is the output vector
A is the state matrix
B is the input matrix
C is the output matrix
D is the feedforward matrix
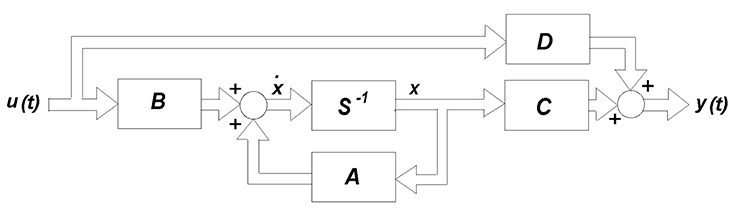
Image credit: wikipedia.org
*A time-invariant system is one in which the output doesn’t depend on when the input occurred. In contrast, in a time-variant system, the timing of the input has an effect on the output. An example of a time-variant system is a dispensing system, where the mass of the system changes as it dispenses the liquid into the process.
State space control is often referred to as a “modern” control method because it takes the differential equations that describe the time domain of the system and analyzes them in vector form using state variables. This makes it possible to evaluate the system via simple matrix algebra, which also allows multiple-input, multiple-output systems to be evaluated. This is in contrast to “classical” control methods, such as PID, which rely on complex Laplace transforms and Fourier transforms to convert the system’s time domain representation – given as a complex set of differential equations – into the frequency domain – given as algebraic equations.
The major benefit of state space control over transfer function methods is its applicability to a wide range of systems: linear and non-linear; time-varying and time-invariant; single-input, single-output (SISO) and multiple-input, multiple-output (MIMO).






Leave a Reply
You must be logged in to post a comment.