FAQ: What’s the difference between torque constant, back EMF constant, and motor constant?

A DC motor’s output torque is directly proportional to the current through the windings, and the motor’s angular speed is directly proportional to the back EMF that it generates. These simple relationships are typically given by the equations:

Where:

T = torque (Nm)

I = current (A)

k_T = torque constant (Nm/A)

And

Where:

ω = angular velocity (rad/s)

V_E = back EMF voltage (V)

k_E = back EMF constant (V-s/rad)

The torque constant, k_T, is specific to motor’s design, including its magnetic strength, number of wire turns, and armature length. The slope of the motor’s torque-current curve is determined by the torque constant.

The back EMF constant, k_E, represents the relationship between the motor’s back EMF and its speed. It has an often-used inverse, referred to as the voltage constant, k_V. The back EMF constant, k_E, is given in units of volt-seconds per radian (V-s/rad), and conversely, the voltage constant, k_V is given in units of radians per volt-second (rad/V-s).

Interestingly, the torque constant, k_T and the back EMF constant, k_E are equal. This can be demonstrated by applying the law of conservation of energy: electrical power in must be equal to mechanical power out plus motor electrical losses.

Typical DC motor circuit
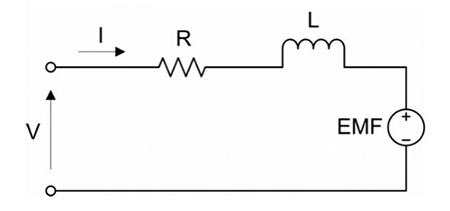
Image credit: Precision Microdrives Limited

Electrical power in is equal to voltage times current.

According to Kirchhoff’s Voltage Law, the applied voltage is given as:

Where:

R = motor resistance (ohms)

Substituting for V_E (from above)

Now, multiplying voltage by current, we get:

Mechanical power out is equal to torque times rotational speed:

Substituting for T (from above):

Electrical losses are caused by the resistance in the circuit:

Now, setting electrical power in equal to mechanical power out plus losses, we get:

You can see that all terms cancel out, except the back EMF constant and the torque constant, which must be equal:

Also related to the torque constant is the motor constant, k_m, which represents the motor’s ability to convert electrical power to mechanical power. The motor constant is given by:

Where:

k_m = motor constant (Nm/√Watt)

T = torque (Nm)

P = resistive power losses (also known as I²R losses) (W)

Substituting for T (from above) and resistive power losses, P, we get:

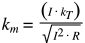
Which simplifies to:

The motor constant is supplied by the manufacturer, and is useful for comparing the relative outputs, or efficiencies, of different motors.