The term “moment of inertia” is often used generically, but depending on the context and application, it can refer to one of three different moments of inertia: mass, planar, or polar. In order to know which one is needed for a given calculation or analysis, it’s important to understand the differences between them and how each one relates to the behavior of an object.
Mass moment of inertia formula
Mass moment of inertia describes the object’s ability to resist angular acceleration, which depends on how the object’s mass is distributed with respect to the axis of rotation (i.e., the object’s shape). Mass moment of inertia is typically denoted as “I,” although “J” is commonly used in engineering references, such as motor or gearbox inertia specifications. Its units are mass-distance squared: kgm2 or lbm-ft2. (Note that slug-ft2 is also sometimes used.)
Image credit: brilliant.org
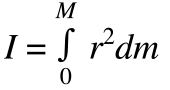
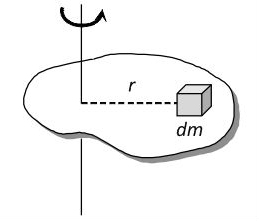
In many applications, an object is modeled as a point mass, and the mass moment of inertia is simply the object’s mass multiplied by the radius (distance to axis of rotation) squared.
Image credit: brilliant.org
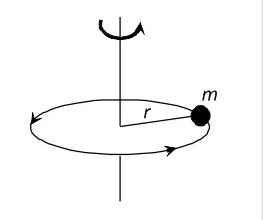
Mass moment of inertia is important for motor sizing, where the inertia ratio — the ratio of the load inertia to the motor inertia — plays a significant role in determining how well the motor can control the load’s acceleration and deceleration.
Planar and polar moments of inertia formulas
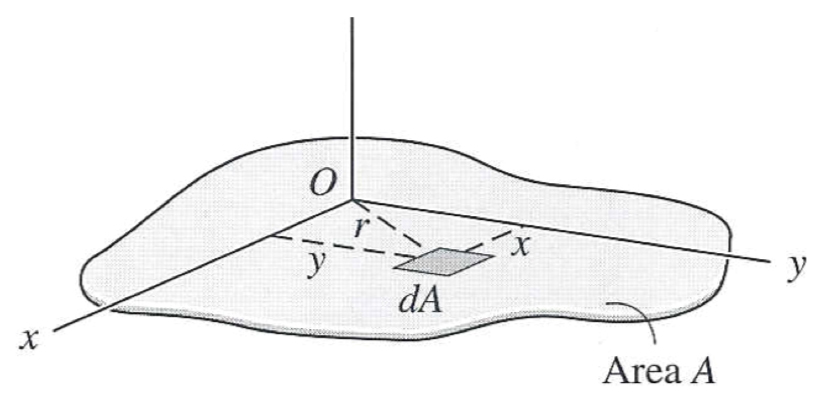
Planar and polar moments of inertia both fall under the classification of “second moment of area.” Planar moment of inertia describes how an area is distributed relative to a reference axis (typically the centroidal, or central, axis). This is important because it specifies the area’s resistance to bending.
The equation for planar moment of inertia takes the second integral of the distance to the reference plane, multiplied by the differential element of area. The result is expressed in units of length to the fourth power: m4 or in4.
Image credit: arizona.edu
Polar moment of inertia is analogous to planar moment of inertia but is applicable to a cylindrical object and describes its resistance to torsion (twisting due to an applied torque).
The equation for polar moment of inertia is essentially the same as that for planar moment of inertia, but in the case of polar moment, distance is measured to an axis parallel to the area’s cross-section. Polar moment of inertia is sometimes denoted with the letter J, instead of I, but its units are the same as those for planar moment of inertia: m4 or in4.
Polar moment of inertia (denoted here as Ip) can also be found by summing the x and y planar moments of inertia (Ix and Iy).
Planar and polar moments of inertia are used when calculating deflection — either linear displacement due to an applied force or angular displacement due to an applied moment.
Leave a Reply
You must be logged in to post a comment.